MPI
The Message Passing Interface (MPI) is an open library standard for distributed memory parallelization. The library API (Application Programmer Interface) specification is available for C and Fortran. There exist unofficial language bindings for many other programming languages, e.g. Python a, b or JAVA 1, 2, 3. The first standard document was released in 1994. MPI has become the de-facto standard to program HPC cluster systems and is often the only way available. There exist many implementations, Open source and proprietary. The latest version of the standard is MPI 3.1 (released in 2015).
MPI allows to write portable parallel programs for all kinds of parallel systems, from small shared memory nodes to petascale cluster systems. While many criticize its bloated API and complicated function interface no alternative proposal could win a significant share in the HPC application domain so far. There exist optimized implementations, open source and proprietary, for any HPC platform and architecture and a wealth of tools and libraries. Common implementations are OpenMPI, mpich and Intel MPI. Because MPI is available for such a long time and almost any HPC application is implemented using MPI it is the safest bet for a solution that will be supported and stable on mid- to long-term future systems.
Information on how to run an existing MPI program can be found in the How to Use MPI Section.
API overview
The standard specifies interfaces to the following functionality (incomplete list):
- Point-to-point communication,
- Datatypes,
- Collective operations,
- Process groups,
- Process topologies,
- One-sided communication,
- Parallel file I/O.
While the standard document has 836 pages describing 500+ MPI functions a working and useful MPI program can be implemented using just a handful of functions. As with other standards new and uncommon features are often initially not implemented efficiently in available MPI libraries.
Basic conventions
An MPI program is written in a sequential programming language. The basic
worker unit in MPI is a process. Processes are assigned consecutive ranks
(integer number) and a process can ask for its rank and the total number
of ranks from within the program. Data exchange and synchronization is
implemented by sending and receiving messages using appropriate library
calls. MPI uses the term communicator for a group of ranks. There exists
a predefined communicator called MPI_COMM_WORLD including all
processes within a job. Communicators only containing a subset of all
ranks can be created at runtime. A communicator is an argument to every
MPI communication routine. In many applications it is sufficient to use
MPI_COMM_WORLD only. The information which ID is the own rank and
how many ranks are there in total is already sufficient to create work
sharing strategies and communication structures. Messages can be send to
another rank using its ID, collective communication (as e.g. broadcast)
involve all processes in a communicator. MPI follows the multiple program
multiple data (MPMD) programming model which allows to use separate source
codes for the different processes. However it is common practice to use
a single source for a MPI application (single program multiple data
(SPMD)).
Point-to-point communication
Sending and receiving of messages by processes is the basic MPI communication mechanism. The basic point-to-point communication operations are send and receive.
MPI_Sendfor sending a message
int MPI_Send (const void* buf, int count, MPI_Datatype datatype, int dest, int tag, MPI_Comm comm)
MPI_Recvfor receiving a message
int MPI_Recv (void* buf, int count, MPI_Datatype datatype, int source, int tag, MPI_Comm comm, MPI_Status* status)
MPI communication routines consist of the message data and a message envelope. The message data is specified by a pointer to a memory buffer, the MPI datatype and a count. Count may be zero to indicate that the message buffer is empty. The message envelope consists of the source (implicitly specified by the sender), destination, tag and communicator. Destination is the id of the receiving process and tag an integer which allows to distinguish different message types.
Above functions (which are normal mode blocking in MPI speak) are the simplest example of point-to-point communication. In the standard there exist two basic flavors of point-to-point comunication: blocking and non-blocking. Blocking means that the communication buffer passed as an argument to the communication routine may be reused after the call returns, whereas in non-blocking the buffer must not be used until a completion test was called (MPI_WAIT or MPI_TEST). One could say that in the non-blocking flavor the potential for asynchronous communication is exposed to the API. Blocking and non-blocking sends and receives can be mixed with each other. To complicate things further the standard introduces different communication modes: normal, buffered, synchronous and ready. Please refer to the references for more details on those topics. While making general recommendation is dangerous one can say that in many cases using the normal non-blocking variant for point-top-point communication is no mistake.
Collective operations
MPI supports collective communication primitives for cases where all ranks are involved in communication. Collective communication does not interfere in any way with point-to-point communication. All ranks within a communicator have to call the routine. While collective communication routines are often necessary and helpful they also may introduce potential scalability problems. Therefore they should be used with great care.
There exist three types of collective communication:
- Synchronization (barrier)
- Data movement (e.g. gather, scatter, broadcast)
- Collective computation (reduction)
Examples for collective communication:
MPI_Bcastfor broadcasting a message
int MPI_Bcast(void* buffer, int count, MPI_Datatype datatype, int root, MPI_Comm comm)
MPI_BCAST broadcasts a message from the process with rank root to all processes of the communicator, itself included. It is called by all members of the communicator using the same arguments for comm and root. On return, the content of root’s buffer is copied to all other processes.
MPI_Reducefor reduction operations
int MPI_Reduce(const void* sendbuf, void* recvbuf, int count, MPI_Datatype datatype, MPI_Op op, int root, MPI_Comm comm)
MPI_REDUCE combines the elements provided in the input buffer of each process in the communicator, using the operation op, and returns the combined value in the output buffer of the process with rank root. The input buffer is defined by the arguments sendbuf, count and datatype; the output buffer is defined by the arguments recvbuf, count and datatype; both have the same number of elements, with the same type. The routine is called by all communicator members using the same arguments for count, datatype, op, root and comm. Thus, all processes provide input buffers of the same length, with elements of the same type as the output buffer at the root.
Examples for MPI programs
Hello World with MPI
A simple Hello world example implemented in C.
#include <stdio.h>
#include <mpi.h>
main(int argc, char **argv)
{
int ierr, num_procs, my_id;
ierr = MPI_Init(&argc, &argv);
ierr = MPI_Comm_rank(MPI_COMM_WORLD, &my_id);
ierr = MPI_Comm_size(MPI_COMM_WORLD, &num_procs);
printf("Hello world! I'm process %i out of %i processes\n",
my_id, num_procs);
ierr = MPI_Finalize();
}
Integration example: Blocking P2P communication
This is a program fragment for Fortran for a parallel integration using blocking point-to-point communication. The integral of a function is computed an existing integrate routine. The interval [a,b] is split into equal disjoint chunks and partial results are computed in parallel. Rank 0 collects all results from all other processes and sums up the result.
integer, dimension(MPI_STATUS_SIZE) :: status
call MPI_Comm_size(MPI_COMM_WORLD, size, ierror)
call MPI_Comm_rank(MPI_COMM_WORLD, rank, ierror)
! integration limits
a=0.d0 ; b=2.d0 ; res=0.d0
! limits for "me"
mya=a+rank*(b-a)/size
myb=mya+(b-a)/size 11
! integrate f(x) over my own chunk - actual work
psum = integrate(mya,myb)
! rank 0 collects partial results
if(rank.eq.0) then
res=psum
do i=1,size-1
call MPI_Recv(tmp, &
1, &
MPI_DOUBLE_PRECISION,&
i, & ! rank of source
0, & ! tag (unused here)
MPI_COMM_WORLD,& ! communicator
status,& ! status array (msg info)
ierror)
res=res+tmp
end do
write(*,*) ’Result: ’,res
! ranks != 0 send their results to rank 0
else
call MPI_Send(psum, & ! send buffer
1, & ! message length
MPI_DOUBLE_PRECISION,&
0, & ! rank of destination
0, & ! tag (unused here)
MPI_COMM_WORLD,ierror)
end if
Integration example: Non-Blocking P2P communication
Above example using non-blocking point-to-point communication. Rank 0 pre-posts all required non-bloking receives, then everybody computes its range. Finally rank 0 waits for all receives to complete, while all other processes send their result using a blocking send.
integer, allocatable, dimension(:,:) :: statuses
integer, allocatable, dimension(:) :: requests
double precision, allocatable, dimension(:) :: tmp
call MPI_Comm_size(MPI_COMM_WORLD, size, ierror)
call MPI_Comm_rank(MPI_COMM_WORLD, rank, ierror)
! integration limits
a=0.d0 ; b=2.d0 ; res=0.d0
if(rank.eq.0) then
allocate(statuses(MPI_STATUS_SIZE, size-1)) allocate(requests(size-1)) allocate(tmp(size-1))
! pre-post nonblocking receives
do i=1,size-1
call MPI_Irecv(tmp(i), 1, MPI_DOUBLE_PRECISION, &
i, 0, MPI_COMM_WORLD, &
requests(i), ierror)
end do
end if
! limits for "me"
mya=a+rank*(b-a)/size
myb=mya+(b-a)/size
! integrate f(x) over my own chunk - actual work
psum = integrate(mya,myb)
! rank 0 collects partial results
if(rank.eq.0) then
res=psum
call MPI_Waitall(size-1, requests, statuses, ierror)
do i=1,size-1
res=res+tmp(i)
end do
write (*,*) ’Result: ’,res
! ranks != 0 send their results to rank 0
else
call MPI_Send(psum, 1, &
MPI_DOUBLE_PRECISION, 0, 0, &
MPI_COMM_WORLD,ierror)
end if
Integration example: Collective communication
And the same example once more using collective communication. This allows for a very compact implementation using just a single
MPI_Reduce called by all ranks.
call MPI_Comm_size(MPI_COMM_WORLD, size, ierror)
call MPI_Comm_rank(MPI_COMM_WORLD, rank, ierror)
! integration limits
a=0.d0 ; b=2.d0 ; res=0.d0
mya=a+rank*(b-a)/size
myb=mya+(b-a)/size
! integrate f(x) over my own chunk
psum = integrate(mya,myb)
call MPI_Reduce(psum, res, 1, &
MPI_DOUBLE_PRECISION, MPI_SUM, &
0, MPI_COMM_WORLD, ierror)
if(rank.eq.0) write(*,*) ´Result: ´,res
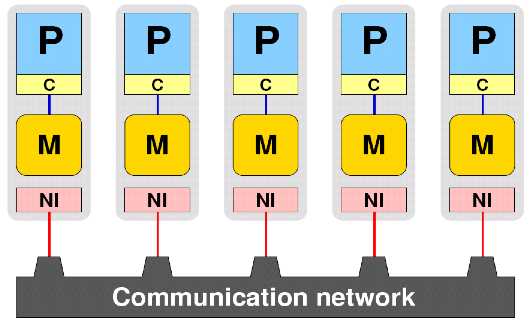
MPI machine model
MPI is using the following machine model:
All processors P do not share any topological entity with each other and are equal with every respect. They are connected using one uniform network. This basic machine model captures all possible parallel machines. Still many performance relevant features of real parallel systems are not represented: Cluster of SMP structure, shared memory hierarchy, shared network interface, network topology. While optimized MPI implementations try to provide the best possible performance for each communication case, the fact that communication between two partners is not equal across a MPI communicator cannot be solved and has to be explicitly addressed by the programmer.
MPI+X
There is often already a large amount of parallelism on the node level. Because MPI's finest granularity process may add significant overhead a common strategy is to mix MPI with some other lightweight programming model on the node level. A common case on a cluster with large shared memory nodes it is natural to combine MPI with OpenMP or any other threaded programming model.
Mixing MPI another programming model in any case adds significant complexity on the implementation level as well as later when running the application. There must therefore be a good reason for going hybrid. If an MPI code scales very well one should not try to be better with an hybrid code.
Common reasons for going hybrid could be:
- Explicitly overlapping communication with computation
- Improve MPI performance through larger messages
- Reuse of data in shared caches
- Easier load balancing with OpenMP
- Exploit additional levels of parallelism (vector processor codes, parallel structures where MPI overhead is too large for parallelization)
- Improve convergence if you parallelize loop-carried dependencies, e.g. domain decomposition with a implicit solver
Alternatives to MPI
There is no doubt that MPI is a bloated, complicated and sometimes confusing library standard. Early on there were efforts to introduce more elegant and productive solutions to program distributed memory systems. Cray was a pioneer introducing the very light weight SHMEM library API, which later was used as basis for implemenations of the partitioned global address space (PGAS) programming model. PGAS assumes a global address space that is logically partitioned and a portion of it is local to each process. Access to non-local address ranges have to be mapped to e.g. network messages. In many implementations PGAS is a part of the language standard and therefore allows for a cleaner and more elegant integration than a libary solution. Examples for PGAS languages are UPC, CoArray Fortran, Chapel and X10.
Hopes that the integration of distributed memory communication into the language allows for advanced optimizations by the compiler or a runtime system were dissapointed. A high performance PGAS program looks very similar to a high performance MPI program but with a nicer implementation interface.
References
MPI language standard. The standard is not suited for learning MPI but is useful as a reference document with many source code examples. Also available as printed books.
Teaching material
- PPCES 2025 (@RWTH Aachen) - Message Passing Basics
- PPCES 2025 (@RWTH Aachen) - MPI Concepts
- PPCES 2025 (@RWTH Aachen) - Blocking Point-to-Point Communication
- PPCES 2025 (@RWTH Aachen) - Non-blocking Point-to-Point Communication
- PPCES 2025 (@RWTH Aachen) - Derived Datatypes
- PPCES 2025 (@RWTH Aachen) - Blocking Collective Communication
- PPCES 2025 (@RWTH Aachen) - Communicator Handling
- PPCES event series (@RWTH Aachen)
Training Events
- NHR-Verein - Courses and Workshops
- HPC.NRW - Event Calendar
- HPC Training Events in Germany
- HPC Training Events in Europe
Textbooks and links
As the MPI standard evolving slowly, even books form the last century are not obsolete, but incomplete (do not contain latest features).
- Marc Snir, Steve Otto, Steven Huss-Lederman, David Walker, Jack Dongarra: "MPI. The Complete Reference Vol. 1: The MPI core." Second edition. MIT Press. ISBN-13: 978-0262692151. The first edition of this book is available online as html version or as postscript version.
- William Gropp, Steven Huss-Lederman, Andrew Lumsdaine, Ewing Lusk, Bill Nitzberg, William Saphir, Marc Snir: "MPI: The Complete Reference. Vol 2: The MPI-2 extensions." - MIT Press - 1998. ISBN-13: 978-0262571234
- Peter Pacheco: "Parallel Programming With MPI" - Morgan Kaufmann Publishers - 1996. ISBN-13: 978-1558603394 is extended from the original 50-page "A User's Guide to MPI" (dead link, copy).
- Peter Sanders, Thomas Worsch: "Parallele Programmierung mit MPI - ein Praktikum" - 150 pages - Logos Verlag - 1997. ISBN-13: 978-3931216764 (in German)
- Using MPI and Using Advanced MPI - The MIT Press - 2014