Difference between revisions of "Performance model"
m |
|||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Category:HPC-Developer]] | ||
| + | [[Category:Benchmarking]]<nowiki /> | ||
| + | |||
There is a wide range of completely different things coined under the term performance model. Here we adopt “the physics way” of using models in computer science, specifically | There is a wide range of completely different things coined under the term performance model. Here we adopt “the physics way” of using models in computer science, specifically | ||
for the interaction between hardware and software. A model in this sense is a “mathematical description” based on a simplified machine model that ignores most of the details of what is going on under the hood; it makes certain assumptions, which must be clearly specified so that the range of applicability of the model is entirely clear. | for the interaction between hardware and software. A model in this sense is a “mathematical description” based on a simplified machine model that ignores most of the details of what is going on under the hood; it makes certain assumptions, which must be clearly specified so that the range of applicability of the model is entirely clear. | ||
| Line 12: | Line 15: | ||
The naïve Roofline is obtained by applying simple bound and bottleneck analysis. In this formulation of the Roofline model, there are only two parameters, the peak performance and the peak bandwidth of the specific architecture, and one variable, the code balance. | The naïve Roofline is obtained by applying simple bound and bottleneck analysis. In this formulation of the Roofline model, there are only two parameters, the peak performance and the peak bandwidth of the specific architecture, and one variable, the code balance. | ||
| − | :<math>P = min(P_\text{peak}, \frac{b_\text{Mem}}{b^\text{Mem}_\text{c}})</math> | + | :<math>P = \min\left(P_\text{peak}, \frac{b_\text{Mem}}{b^\text{Mem}_\text{c}}\right)</math> |
where <math>P</math> is the attainable performance, <math>P_\text{peak}</math> is the peak performance, <math>b_\text{Mem}</math> is the peak bandwidth and <math>b^\text{Mem}_\text{c} = V_\text{Mem}/W</math> is the code balance, where <math>W</math> is the number of flops in the loop (i.e., the amount of “work”) and <math>V_\text{Mem}</math> is the amount of | where <math>P</math> is the attainable performance, <math>P_\text{peak}</math> is the peak performance, <math>b_\text{Mem}</math> is the peak bandwidth and <math>b^\text{Mem}_\text{c} = V_\text{Mem}/W</math> is the code balance, where <math>W</math> is the number of flops in the loop (i.e., the amount of “work”) and <math>V_\text{Mem}</math> is the amount of | ||
| Line 25: | Line 28: | ||
This relation can be visualized in a graphical representation: | This relation can be visualized in a graphical representation: | ||
| + | |||
| + | [[File:Roofline-model.png|600px]] | ||
The machine parameters in the roofline formula determine a function <math>P(B_\text{c})</math> that is specific for a given machine, and from which | The machine parameters in the roofline formula determine a function <math>P(B_\text{c})</math> that is specific for a given machine, and from which | ||
| Line 63: | Line 68: | ||
* Wikipedia article on the [https://en.wikipedia.org/wiki/Roofline_model Roofline model] | * Wikipedia article on the [https://en.wikipedia.org/wiki/Roofline_model Roofline model] | ||
* Introduction to the [https://hpc.fau.de/research/ecm/ ECM model] | * Introduction to the [https://hpc.fau.de/research/ecm/ ECM model] | ||
| − | * [Hofm2018] J. Hofmann, G. Hager, and D. Fey: On the accuracy and usefulness of analytic energy models for contemporary multicore processors. In: R. Yokota, M. Weiland, D. Keyes, and C. Trinitis (eds.): High Performance Computing: 33rd International Conference, ISC High Performance 2018, Frankfurt, Germany, June 24-28, 2018, Proceedings, Springer, Cham, LNCS 10876, ISBN 978-3-319-92040-5 (2018), 22-43. DOI: [https://dx.doi.org/10.1007/978-3-319-92040-5_2 10.1007/978-3-319-92040-5_2], Preprint: [https://arxiv.org/abs/1803.01618 arXiv:1803.01618]. Winner of the ISC 2018 Gauss Award. | + | * [Hofm2018] J. Hofmann, G. Hager, and D. Fey: On the accuracy and usefulness of analytic energy models for contemporary multicore processors. In: R. Yokota, M. Weiland, D. Keyes, and C. Trinitis (eds.): High Performance Computing: 33rd International Conference, ISC High Performance 2018, Frankfurt, Germany, June 24-28, 2018, Proceedings, Springer, Cham, LNCS 10876, ISBN 978-3-319-92040-5 (2018), 22-43. DOI: [https://dx.doi.org/10.1007/978-3-319-92040-5_2 10.1007/978-3-319-92040-5_2], Preprint: [https://arxiv.org/abs/1803.01618 arXiv:1803.01618]. Winner of the ISC 2018 Gauss Award. (The most recent incarnation of the ECM model) |
| + | * H. Stengel, J. Treibig, G. Hager, and G. Wellein: Quantifying performance bottlenecks of stencil computations using the Execution-Cache-Memory model. Proc. ICS15, the 29th International Conference on Supercomputing, June 8-11, 2015, Newport Beach, CA. DOI: [http://dx.doi.org/10.1145/2751205.2751240 10.1145/2751205.2751240]. '''Recommended as a good starting point to learn about the ECM model'''. | ||
| + | * G. Hager, J. Treibig, J. Habich, and G. Wellein: Exploring performance and power properties of modern multicore chips via simple machine models. Concurrency and Computation: Practice and Experience 28(2), 189-210 (2016). First published online December 2013, DOI: [http://dx.doi.org/10.1002/cpe.3180 10.1002/cpe.3180]. | ||
Latest revision as of 12:28, 19 July 2024
There is a wide range of completely different things coined under the term performance model. Here we adopt “the physics way” of using models in computer science, specifically for the interaction between hardware and software. A model in this sense is a “mathematical description” based on a simplified machine model that ignores most of the details of what is going on under the hood; it makes certain assumptions, which must be clearly specified so that the range of applicability of the model is entirely clear.
Introduction
For performance engineering the focus is on resource-based analytic loop performance models. To formulate a performance model generates knowledge about software-hardware interaction. Its main purpose is to come up with a quantitative estimate for an expected performance. Without an expected performance estimate it is impossible to decide on performance optimizations as there is no clear knowledge what aspect of software/hardware interaction limits the performance and what could be the optimal performance. An example process employing performance modelling is the performance Performance Patterns based performance engineering process. You formulate a model to estimate expected performance and compare this to application benchmarking. Additionally performance profiling may be used to validate model predictions. In case the validation fails either the profiling or performance measurement are wrong, the model assumptions are not met or the model inputs are wrong. During the process to bring the model estimate and the measured in-line the knowledge about software-hardware interaction is increased and therefore the trust in the performance analysis. It is clear that you will not set up a performance model for every loop kernel. And of course you can do a meaningful performance analysis without a model, e.g. based on rough upper limit estimates. Still for deciding on major code optimizations a model can give you the required confidence that you make a deliberate decision.
One premise that is often valid in scientific computing is the steady state assumption: Most programs comprise loops that are much longer than typical pipeline lengths or other hardware latencies. The execution in each of those loops can be seen as continuous streams of data (input and/or output) being manipulated by a continuous, periodic stream of instructions. The two resources offered by stored-program computers are: executing instructions and transferring data. The complexity in finding out the light-speed performance of a loop kernel on a specific processor is caused by the fact that the execution as well as data transfer rate is specific for the the code executed. The most popular model with this respect is the roofline model, whose basic concepts had been in use since the late 1980s (coined under the term balance metric). It was popularized and refined by Sam Williams in 2009.
Roofline model
The naïve Roofline is obtained by applying simple bound and bottleneck analysis. In this formulation of the Roofline model, there are only two parameters, the peak performance and the peak bandwidth of the specific architecture, and one variable, the code balance.
where is the attainable performance, is the peak performance, is the peak bandwidth and is the code balance, where is the number of flops in the loop (i.e., the amount of “work”) and is the amount of data transferred through the memory interface. The code balance, i.e., a single number, is the part of the roofline model describing the code (the application model), while and characterize the machine (the machine model). Despite these bold simplifications, the strictly light-speed predictions of the model are not only absolute upper bounds but also accurate to a useful degree in many cases. In order to determine its area of applicability we have to state clearly the assumptions that go into it:
- Steady state assumption. This applies to practically all performance models: Start-up and wind-down effects can be neglected, and a continuous stream of instructions and data is processed by the CPU.
- Overlap assumption. Data transfers and arithmetic code execution overlap perfectly. As a consequence, the “slowest bottleneck” wins, no matter by which margin, and there is no interaction between bottlenecks.
- No-latency assumption. Data paths work at their highest achievable bandwidth, and latency effects are ignored.
- Saturation assumption. It must be possible, on the hardware at hand, to actually saturate the memory bandwidth.
The most crucial of these in view of the roofline model is certainly the overlap assumption. In fact, if we accept above formulation as a predictive model for runtime, we have to presume full overlap as well. The saturation assumption leads to an important consequence for practical applications: Since a single core can often not saturate the memory bandwidth of a chip, the model is best applied to the full chip, i.e, P peak is the full-chip (all cores) peak performance, and all bandwidth numbers pertain to the full chip as well.
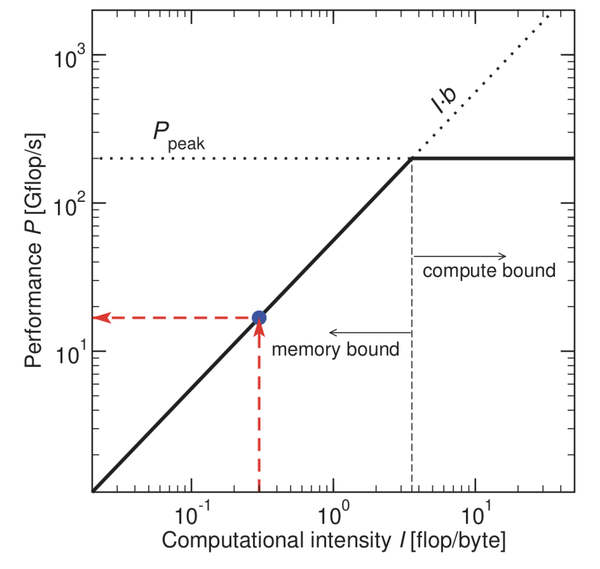
This relation can be visualized in a graphical representation:
The machine parameters in the roofline formula determine a function that is specific for a given machine, and from which the performance limit can be read off easily for any value of . For historical reasons we use intensity, on the x axis the reciprocal of the memory code balance, , the computational intensity so that the performance function reads . The Figure shows clearly how this representation came to serve as a name giver for the model. The upper limit (drawn as a solid line) has two branches, or ceilings: At low intensity (i.e., high code balance), where P = I ·b, performance is linear in with a slope of b. Increasing the intensity (i.e., reducing the code balance) leads to a proportional gain in performance. This is the memory-bound ceiling, where the code does little work for every byte of data and is thus limited by memory bandwidth. At high intensity (i.e., low code balance), we get because the code is busy doing arithmetic with little “hunger” for data, and the memory interface can keep up. This is the compute-bound ceiling. Note that the roofline diagram is usually drawn with logarithmic scales. This has the interesting consequence that a change in memory bandwidth, which would lead to a different slope in a linear graph, causes a parallel shift of the bandwidth ceiling.
There are many refinements of the roofline model, e.g. taking into account the real instruction code for and also adopt the roof accordingly.
ECM model
The ECM model can be seen as a generalized form of the roofline model. It can be applied to predict single-core and in-cache performance as well as multicore scaling. Due to heuristics used to predict overlap among runtime contributions the model in opposite to the roofline model does not provide a light-speed prediction.
The ECM (Execution-Cache-Memory) performance model is also a resource-based analytic performance model. It can predict the runtime of serial straight-line code (usually an inner-most loop body) on a specific processor chip. Runtime predictions are based on a maximum throughput assumptions for instruction execution as well as data transfers, but refinements can be added. The model in its simplest form can be set up with pen and paper.
The model decomposes the overall runtime into several contributions, which are then put together according to a machine model. A processor cycle is the only time unit used. All runtime contributions are provided for a number of instructions required to process a certain number of (source) loop iterations; one typically chooses one cache line length (e.g., 8 iterations for a double precision code), which makes sense because the smallest unit of data that can be transferred between memory hierarchy levels is a cache line. For simple calculations bandwidths and performance are consistently specified in “cycles per cache line.” However, this choice is essentially arbitrary, and one could just as well use “cycles per iteration.” Unless otherwise specified, an “iteration” is one iteration in the high-level code.
The primary resource provided by a CPU core is instruction execution. Since instructions can only be executed when their operands are available, the in-core part of the ECM model assumes that all data resides in the innermost cache. It further assumes out-of-order scheduling and speculative execution to work perfectly so that all the instruction-level parallelism available in the code can be provided by the hardware, resources permitting (on a given microarchitecture).
In practice, the first step is to ignore all influences preventing maximum instruction throughput, such as:
- Out-of-order limitations
- Instruction fetch issues
- Instruction decoding issues
- Complex register dependency chains
Loop-carried dependencies and long latency instructions should be considered, though. The in-core model thus delivers an optimistic execution time for the code (in cycles per iteration) in which all data transfers beyond the innermost cache are ignored.
Data transfers are a secondary resource required by code execution. Modeling data transfers starts with an analysis of the data volume transferred over the various data paths in the memory hierarchy. Some knowledge about the CPU architecture is required for this in order to know what path cache lines take to get from their initial location into L1 cache and back. It is assumed that latencies can be perfectly hidden by prefetching, so all transfers are bandwidth limited. Additional data transfers from cache conflicts are neglected (it is still possible to extend the model to account for additional transfers). Together with known (or measured) maximum bandwidths, the data transfer analysis results in additional runtime contributions from every data path. How to put together these contributions with each other and with the in-core execution time is part of the machine model. The two extreme cases are:
- Full overlap: The predicted execution time is the maximum of all contributions.
- No overlap: The predicted execution time is the sum of all contributions
There is s large gray zone in between these extremes. On most modern Intel Xeon CPUs, data transfer times must be added up and everything that pertains to “work” (i.e., arithmetic, loop mechanics, etc.) overlaps with data transfers. This yields the most accurate predictions on these CPUs, but other architectures behave differently.
If the characteristics of a processor are too poorly understood to come up with a useful machine model, one can assume “best case” and “worst case” scenarios, which may translate to the “full overlap” and “no overlap” models described above. In many cases the predictions thus made will be too far apart to be useful, though. A machine model will always contain some heuristics to make it work in practice. Note that the goal here is always to have a model that has predictive power. Whether or not some “(non-)overlap” assumptions are actually implemented in the hardware is an entirely different matter. In other words, the model may be wrong (because it is based on false assumptions) but still useful in terms of predictive power.
The extension to multi-core is straightforward. The one core performance is scaled linearly until a shared bottleneck in the processor design is hit. This may be a shared cache or memory interface. The ECM model can predict if a code is able to saturate the memory bandwidth and how many cores are required to do so. The model has recently been extended to describe deviations from this simple behavior with great accuracy [Hofm2018].
Links and further information
- Wikipedia article on the Roofline model
- Introduction to the ECM model
- [Hofm2018] J. Hofmann, G. Hager, and D. Fey: On the accuracy and usefulness of analytic energy models for contemporary multicore processors. In: R. Yokota, M. Weiland, D. Keyes, and C. Trinitis (eds.): High Performance Computing: 33rd International Conference, ISC High Performance 2018, Frankfurt, Germany, June 24-28, 2018, Proceedings, Springer, Cham, LNCS 10876, ISBN 978-3-319-92040-5 (2018), 22-43. DOI: 10.1007/978-3-319-92040-5_2, Preprint: arXiv:1803.01618. Winner of the ISC 2018 Gauss Award. (The most recent incarnation of the ECM model)
- H. Stengel, J. Treibig, G. Hager, and G. Wellein: Quantifying performance bottlenecks of stencil computations using the Execution-Cache-Memory model. Proc. ICS15, the 29th International Conference on Supercomputing, June 8-11, 2015, Newport Beach, CA. DOI: 10.1145/2751205.2751240. Recommended as a good starting point to learn about the ECM model.
- G. Hager, J. Treibig, J. Habich, and G. Wellein: Exploring performance and power properties of modern multicore chips via simple machine models. Concurrency and Computation: Practice and Experience 28(2), 189-210 (2016). First published online December 2013, DOI: 10.1002/cpe.3180.