Difference between revisions of "Load Balancing"
m |
|||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | This is a short overview over the basic concepts of Load Balancing. Load Balancing should be taken into account whenever trying to improve a program's performance by parallelization ([[Parallel_Programming]]). | + | [[Category:HPC-Developer]] |
| + | This is a short overview over the basic concepts of Load Balancing. Load Balancing should be taken into account whenever trying to improve a program's performance by parallelization ([[Parallel_Programming|parallel programming]]). | ||
__TOC__ | __TOC__ | ||
| Line 6: | Line 7: | ||
Parallelization is used to achieve a speedup of the runtime of a program while using the available processors as efficiently as possible. The most common first approach is to parallelize loops in the program, as they usually have a high impact on the runtime. Tools like [[Intel VTune]] can be used to find so-called hotspots in a program. | Parallelization is used to achieve a speedup of the runtime of a program while using the available processors as efficiently as possible. The most common first approach is to parallelize loops in the program, as they usually have a high impact on the runtime. Tools like [[Intel VTune]] can be used to find so-called hotspots in a program. | ||
| − | When splitting the workload across multiple processors, the speedup describes the achieved reduction of the runtime compared to the serial version. Obviously, the higher the speedup, the better. However, the effect of increasing the number of processors usually goes down at a certain point when they cannot be utilized optimally anymore. This parallel efficiency is defined as the achieved speedup divided by the number of processors used. It usually is not possibly to achieve a speedup equal to the number of processors used as most applications have strictly serial parts (Amdahl's Law). | + | When splitting the workload across multiple processors, the speedup describes the achieved reduction of the runtime compared to the serial version. Obviously, the higher the speedup, the better. However, the effect of increasing the number of processors usually goes down at a certain point when they cannot be utilized optimally anymore. This parallel efficiency is defined as the achieved speedup divided by the number of processors used. It usually is not possibly to achieve a speedup equal to the number of processors used as most applications have strictly serial parts ([[Amdahl's_Law|Amdahl's Law]]). |
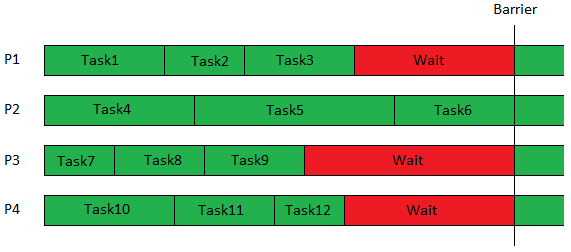
| − | Load balancing is of great importance when utilizing multiple processors as efficient as possible. Adding more processors creates a noticable amount of synchronisation overhead. Therefore, it is only beneficial if there is enough work present to keep all processors busy at the same time. This means | + | Load balancing is of great importance when utilizing multiple processors as efficient as possible. Adding more processors creates a noticable amount of synchronisation overhead. Therefore, it is only beneficial if there is enough work present to keep all processors busy at the same time. This means tasks should not be assigned randomly as this might lead to serial behaviour where only one processor is working while the others have already finished their tasks, e.g. at synchronisation points (e.g. barriers) or at the end of the program. |
| − | == | + | [[File:LoadBalancing.png]] |
| + | |||
| + | == Examples == | ||
| + | |||
| + | '''Example 1:''' | ||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| Line 20: | Line 25: | ||
We assume that there are no data dependencies within the loop. Let the runtime of this loop with 1 processor be 60s. If we split the loop into 2 halves (e.g. i=0-511; i=512-1023) over 2 processors we can expect the runtime to be halved (30s), which would be a speedup of 2 and a perfect efficiency of 1. As the number of instructions is the same for every i it does not matter how we split the loop as long as we split it into equal sizes (ignoring data access optimization, which is not covered here). However, not every loop (or other code snippet) can be distributed this easily. | We assume that there are no data dependencies within the loop. Let the runtime of this loop with 1 processor be 60s. If we split the loop into 2 halves (e.g. i=0-511; i=512-1023) over 2 processors we can expect the runtime to be halved (30s), which would be a speedup of 2 and a perfect efficiency of 1. As the number of instructions is the same for every i it does not matter how we split the loop as long as we split it into equal sizes (ignoring data access optimization, which is not covered here). However, not every loop (or other code snippet) can be distributed this easily. | ||
| − | |||
<syntaxhighlight lang="c"> | <syntaxhighlight lang="c"> | ||
| + | #pragma omp parallel for schedule(static) | ||
for(int i=0; i<1024; i++){ | for(int i=0; i<1024; i++){ | ||
| − | + | dosomething(); | |
| − | |||
| − | |||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | + | Static scheduling divides a loop into chunks as equally as possible (by number of iteration, NOT actual workload). Using 4 processors, these chunks would be (0,255), (256,511), (512,767), (768,1023). Assuming dosomething() does not include critical sections and can be run in parallel all 4 processors should finish almost simultaneously. | |
| − | |||
| − | + | '''Example 2:''' | |
| − | + | <syntaxhighlight lang="c"> | |
| + | for(int i=0; i<1024; i++){ | ||
| + | for(int j=0; j<i+1; j++){ | ||
| + | dosomething(); | ||
| + | } | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| − | + | This loop is obviously more complex. With increasing i the size of the inner loop increases. Simply splitting it in the middle would result in one processor receiving much less work and therefore finishing much earlier than the other processor. While this would still result in a small speedup, it would have a very low efficiency as we are basically wasting resources by letting one processor idle. More complex loops therefore require different strategies in terms of load balancing, for example handing every processor only small chunks at a time. | |
| − | + | <syntaxhighlight lang="c"> | |
| − | + | #pragma omp parallel for schedule(dynamic, 16) | |
| − | + | for(int i=0; i<1024; i++){ | |
| − | + | for(int j=0; j<i+1; j++){ | |
| − | + | dosomething(); | |
| − | + | } | |
| − | + | } | |
| − | + | </syntaxhighlight> | |
| − | + | In this case, static scheduling would lead to the processors finishing in ascending order, the last iterations running completely serial. Therefore it would be more efficient to use dynamic scheduling, where chunks of a chosen size (default 1) are handed out to every waiting processor. Once a processor has finished with its chunk it will be assigned a new one. This way, all processors should be kept running as long as possible. The chunksize has to be chosen carefully, if too small the introduced overhead is larger than the gain, if too large the distribution is less balanced. | |
| − | |||
Latest revision as of 14:49, 3 September 2019
This is a short overview over the basic concepts of Load Balancing. Load Balancing should be taken into account whenever trying to improve a program's performance by parallelization (parallel programming).
General
Parallelization is used to achieve a speedup of the runtime of a program while using the available processors as efficiently as possible. The most common first approach is to parallelize loops in the program, as they usually have a high impact on the runtime. Tools like Intel VTune can be used to find so-called hotspots in a program.
When splitting the workload across multiple processors, the speedup describes the achieved reduction of the runtime compared to the serial version. Obviously, the higher the speedup, the better. However, the effect of increasing the number of processors usually goes down at a certain point when they cannot be utilized optimally anymore. This parallel efficiency is defined as the achieved speedup divided by the number of processors used. It usually is not possibly to achieve a speedup equal to the number of processors used as most applications have strictly serial parts (Amdahl's Law).
Load balancing is of great importance when utilizing multiple processors as efficient as possible. Adding more processors creates a noticable amount of synchronisation overhead. Therefore, it is only beneficial if there is enough work present to keep all processors busy at the same time. This means tasks should not be assigned randomly as this might lead to serial behaviour where only one processor is working while the others have already finished their tasks, e.g. at synchronisation points (e.g. barriers) or at the end of the program.
Examples
Example 1:
for(int i=0; i<1024; i++){
dosomething();
}
We assume that there are no data dependencies within the loop. Let the runtime of this loop with 1 processor be 60s. If we split the loop into 2 halves (e.g. i=0-511; i=512-1023) over 2 processors we can expect the runtime to be halved (30s), which would be a speedup of 2 and a perfect efficiency of 1. As the number of instructions is the same for every i it does not matter how we split the loop as long as we split it into equal sizes (ignoring data access optimization, which is not covered here). However, not every loop (or other code snippet) can be distributed this easily.
#pragma omp parallel for schedule(static)
for(int i=0; i<1024; i++){
dosomething();
}
Static scheduling divides a loop into chunks as equally as possible (by number of iteration, NOT actual workload). Using 4 processors, these chunks would be (0,255), (256,511), (512,767), (768,1023). Assuming dosomething() does not include critical sections and can be run in parallel all 4 processors should finish almost simultaneously.
Example 2:
for(int i=0; i<1024; i++){
for(int j=0; j<i+1; j++){
dosomething();
}
}
This loop is obviously more complex. With increasing i the size of the inner loop increases. Simply splitting it in the middle would result in one processor receiving much less work and therefore finishing much earlier than the other processor. While this would still result in a small speedup, it would have a very low efficiency as we are basically wasting resources by letting one processor idle. More complex loops therefore require different strategies in terms of load balancing, for example handing every processor only small chunks at a time.
#pragma omp parallel for schedule(dynamic, 16)
for(int i=0; i<1024; i++){
for(int j=0; j<i+1; j++){
dosomething();
}
}
In this case, static scheduling would lead to the processors finishing in ascending order, the last iterations running completely serial. Therefore it would be more efficient to use dynamic scheduling, where chunks of a chosen size (default 1) are handed out to every waiting processor. Once a processor has finished with its chunk it will be assigned a new one. This way, all processors should be kept running as long as possible. The chunksize has to be chosen carefully, if too small the introduced overhead is larger than the gain, if too large the distribution is less balanced.