Plotting and Interpreting Results
| Tutorial | |
|---|---|
| Title: | Benchmarking & Scaling |
| Provider: | HPC.NRW
|
| Contact: | tutorials@hpc.nrw |
| Type: | Online |
| Topic Area: | Performance Analysis |
| License: | CC-BY-SA |
| Syllabus
| |
| 1. Introduction & Theory | |
| 2. Interactive Manual Benchmarking | |
| 3. Automated Benchmarking using a Job Script | |
| 4. Automated Benchmarking using JUBE | |
| 5. Plotting & Interpreting Results | |
Strong Scaling
For the strong scaling results we used the example job script as shown in the previous chapter and ran it for all three systems with and without enabled hyperthreading. To plot the results we can write a simple Python script. For this purpose we are making use of the numpy and matplotlib Python libraries. You can of course use any other software to visualize the results.
#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt
# Read in raw data (col1: cores col2: time)
data = np.loadtxt("results_5NM_strong_scaling_noHT.dat")
# Get the mean time for every 5 data points
times = np.mean(data[:,1].reshape(-1, 5), axis=1)
# Get the "mean" no of processes
nprocs = np.mean(d_5NM_NOHT[:,0].reshape(-1, 5), axis=1)
# Calculate the speedup; last time in the "times" array is the serial timing
speedup = times[-1]/times
# Plot
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(nprocs, speedup, '-x', label="5NM - no HT")
ax.legend()
ax.set_xlabel("processors")
ax.set_ylabel("speedup")
ax.set_title("strong scaling")
# Save the figure
fig.savefig("strong_scaling_plot.png", dpi=300)
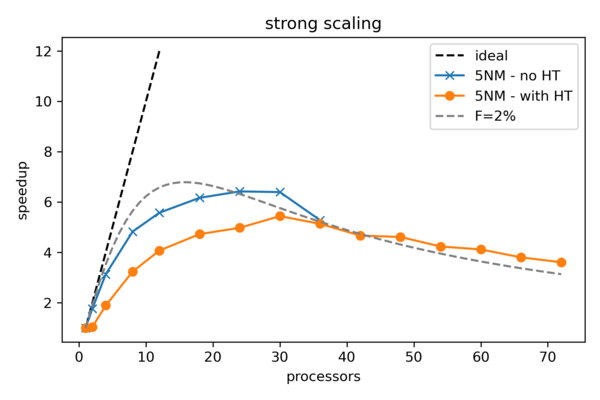
In the plot below, you can see the results for the small 5NM system with and without enabled hyper-threading as well as the theoretical behavior for a code with a serial fraction of around 2%. The first thing we notice, is that the simulation does not benefit from using hyper-threading - even worse, the performance degrades. This does, however, not mean that this is always the case. Some codes can actually benefit from using it. The comparison to the theoretical curve with F=2%, tells us that the GROMACS code is fairly well parallelized. We can also observe, that there is no substantial gain in speedup after using more than 24 cores for this system. So when creating a production job with this system, we would limit the number of cores to 24 to not waste any resources.
Weak Scaling
The results for the weak scaling example were obtained by running the simulation for the 5NM, 10NM and 15NM systems using using 9, 18 and 36 cores, respectively. A serial run with one core for each system was performed as a reference. Each run was repeated five times. The bash/job script can be found below:
#!/bin/bash
# Load all needed modules (adjust to your specific site!)
module load GROMACS
GMX="gmx_mpi -nobackup -quiet mdrun -nsteps 10000 -ntomp 1"
GMX5="${GMX} -deffnm MD_5NM_WATER"
GMX10="${GMX} -deffnm MD_10NM_WATER"
GMX15="${GMX} -deffnm MD_15NM_WATER"
echo "# Cores Time/s"
for N in 1 9; do
for i in $(seq 5); do
START=$(date +%s.%N)
srun -n $N $GMX5 > gromacs.log 2>&1
END=$(date +%s.%N)
RUNTIME=$(echo "$END - $START" | bc -l)
printf "%3d %5.2f\n" $N $RUNTIME
done
done
for N in 1 18; do
for i in $(seq 5); do
START=$(date +%s.%N)
srun -n $N $GMX10 > gromacs.log 2>&1
END=$(date +%s.%N)
RUNTIME=$(echo "$END - $START" | bc -l)
printf "%3d %5.2f\n" $N $RUNTIME
done
done
for N in 1 36; do
for i in $(seq 5); do
START=$(date +%s.%N)
srun -n $N $GMX15 > gromacs.log 2>&1
END=$(date +%s.%N)
RUNTIME=$(echo "$END - $START" | bc -l)
printf "%3d %5.2f\n" $N $RUNTIME
done
done
The results are listed below:
# Cores Time/s
1 62.58
1 62.46
1 61.90
1 62.06
1 62.33
9 13.52
9 13.50
9 14.99
9 13.61
9 13.42
1 533.24
1 528.78
1 527.26
1 538.61
1 532.99
18 53.02
18 52.34
18 52.60
18 52.00
18 53.11
1 1881.80
1 1871.87
1 1867.41
1 1864.70
1 1864.01
36 102.71
36 101.77
36 102.08
36 102.98
36 102.36
We can again write a simple Python script to process and plot the resulting data.
Example Python script to plot weak scaling results:
#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt("results_weak_scaling.dat")
# Different set every 10 data points (5 serial + 5 parallel)
wat05 = data[0:10]
wat10 = data[10:20]
wat15 = data[20:30]
wat = [wat05, wat10, wat15]
# Calculate the mean times for every set
stimes = []
ptimes = []
for d in wat:
stimes.append(np.mean(d[0:5], axis=0))
ptimes.append(np.mean(d[5:10], axis=0))
# Re-transform to numpy array
stimes = np.asarray(stimes)
ptimes = np.asarray(ptimes)
# Calculate speedup
speedup = stimes[:,1]/ptimes[:,1]
# Get the No of processors
nprocs = ptimes[:,0]
# Plot
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(nprocs, speedup, '--o', label="speedup")
ax.plot(nprocs, nprocs, '--', color='gray', label="ideal")
ax.legend()
ax.set_xlabel("processors")
ax.set_ylabel("speedup")
ax.set_title("weak scaling")
for x,y,label in zip(nprocs, speedup,["5NM","10NM","15NM"]):
ax.annotate(label, xy=(x,y), textcoords="offset points", xytext=(-12,10))
fig.savefig("weak_scaling_plot.png", dpi=300)
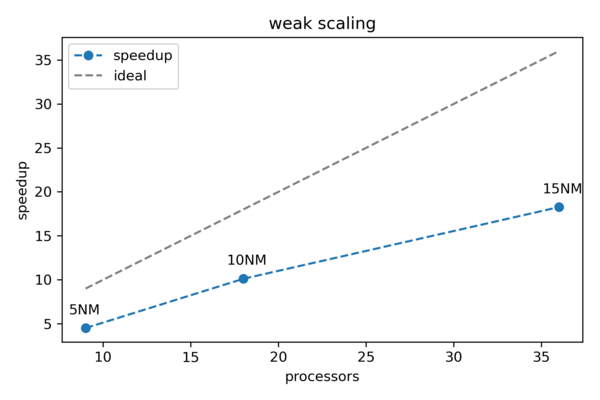
The resulting figure can be seen below. As expected a real-world example does not behave as perfectly as predicted by Gustafson's law. However, we can still observe a close to linear behavior.